李群和李代数
问题的引入
当我们估计出相机姿态$[R, t]$了以后,估计的结果和实际的相机姿态肯定会有一些不一致性,因而我们需要对估计出来的结果进行优化。优化方法一般都采用迭代优化的方法,每次迭代都更新一个位姿的增量$\Delta$,使得目标函数最小。这个$\Delta$就是通过误差函数对$\mathbf{T}$或者$\mathbf{R}$求微分得到的,也就是说我们需要对变换矩阵$\mathbf{T}$以及旋转矩阵$\mathbf{R}$求导。
但是,旋转矩阵并没有良好定义的加法,即$R_1$和$R_2$是都是旋转矩阵,但是$R_1 + R_2$并不符合旋转矩阵的定义:旋转矩阵应该满足$RR^T = I$,且$det(R) = 1$,即行列式的值为1的正交矩阵,因此上边的结论是显而易见的。
所以,在实际操作中,我们无法通过如下的微调满足我们对相机观测模型的优化:
\[[R, t] \stackrel{\Delta R, \Delta t}{\longrightarrow} [R', t'] \\ t' = t + \Delta t \\ R' = R + \Delta R\]因而也会影响到观测模型(关于旋转矩阵的函数)对$\mathbf{R}$的求导,因为通常来说我们的导数定义为:
\[U(R) = \frac{dU}{dR} = \lim\limits_{\Delta R \to 0}\frac{U(R + \Delta R) - U(R)}{\Delta R}\]没有良好定义的加法——没有传统意义上的导数定义。 因此,李群和李代数的作用就是间接对$\mathbf{R}$进行求导。
预备知识
矩阵指数
首先要引入矩阵指数的概念(Matrix Exponential)。矩阵指数可以由线性微分方程的解的形式导出,比如有一阶线性微分方程:
\[\stackrel{·}{x} = ax(t)\]其中,$x(t) \in \mathbb{R}$,$a \in \mathbb{R}$,并且初始分布为$x(0) = x_0$,那么解为:
\[x(t) = e^{at}x_0\]其中指数函数可以展开为无穷级数:
\[e^{at} = 1 + at + \frac{(at)^2}{2!} + \frac{(at)^3}{3!} + ···\]同理,如果我们对三维向量由一阶线性微分方程:
\[\stackrel{·}{x}(t) = Ax(t)\]其中$x(t) \in \mathbb{R}^3$,$A \in \mathbb{R}^{3 \times 3}$,且初始条件为$x(0) = x_0$,那么解为:
\[\\ x(t) = e^{At}x_0\]其中矩阵指数函数可以展开为无穷级数的形式:
\[\\ e^{At} = I + At + \frac{(At)^2}{2!} + \frac{(At)^3}{3!} + ···\]矩阵指数与矩阵旋转的关系
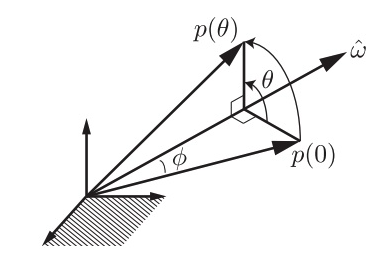
如上图,三维向量$p(0)$绕着单位旋转轴$\hat{\omega}$ ($\hat{\omega} \in \mathbb{R}^3$,$\vert\vert \hat\omega \vert\vert = 1$)旋转$\theta$角度,得到三维向量 $p(\theta)$。该旋转运动亦可以视作是三维向量$p(0)$以$1rad/s$的角速度绕着单位旋转轴$\hat{\omega}$从时间$t = 0$ 运动到时间 $t = \theta$得到三维向量$p(\theta)$。
如果用$p(t)$来表示旋转路径上向量端点处的位置,用$\stackrel{·}{p}(t)$表示该点的瞬时速度值,则有:
\[\stackrel{·}{p} = \hat{\omega} \times p\]而向量叉乘可以写为左端向量对应的反对称矩阵与右端向量的乘积形式:
\[\stackrel{·}{p} = [\hat{\omega}]p\]其中,定义$[·]$为反对称矩阵算子,假如$\hat{\omega} = \begin{Bmatrix} \omega_1 \ \omega_2 \ \omega_3 \end{Bmatrix}$,那么有:
\[[\omega] = \begin{bmatrix} 0 & -\omega_{3} & \omega_{2} \\ \omega_{3} & 0 & -\omega_{1} \\ -\omega_{2} & \omega_{1} & 0 \end{bmatrix}\]那么上式就有如下解:
\[p(t) = e^{[\hat\omega]t}p(0)\]因为角速度为$1rad/s$,所以这里角度$\theta$和时间$t$是可以互换的:
\[p(t) = e^{[\hat\omega]\theta}p(0)\]由于反对称矩阵有满足${[\hat\omega]}^3 = -[\hat\omega]$,将矩阵指数函数展开有:
\[\begin{align} e^{[\hat\omega]\theta} &= I + [\hat\omega]\theta + [\hat\omega]^2\frac{\theta ^ 2}{2!} + [\hat\omega]^3\frac{\theta ^ 3}{3!} + ··· \\ &= I + (\theta - \frac{\theta ^ 3}{3!} + \frac{\theta ^ 5}{5!} - ···)[\hat\omega] + (\frac{\theta ^ 2}{2!} - \frac{\theta ^ 4}{4!} + \frac{\theta ^ 6}{6!}-···)[\hat\omega] ^ 2 \\ &= I + \sin{\theta}[\hat\omega] + (a-\cos{\theta})[\hat\omega] ^ 2 \end{align}\]因此,三维旋转矩阵$R$就可以用矩阵指数$e^{[\hat{\omega}]\theta}$的形式来表示。
李群和李代数
群
群是一种集合加上一种代数运算。这个集合和运算应该满足“封结幺逆”四个性质,把集合记为 $\mathbf{A}$ ,运算记为$\cdot$, 群就可以记为 $\mathbf{G}=(\mathbf{A},\cdot)$。
- 封闭性:$\forall a_1,a_2 \in \mathbf{A},a_1 \cdot a_2 \in \mathbf{A}$
- 结合律:$\forall a_1,a_2,a_3 \in \mathbf{A}, (a_1 \cdot a_2) \cdot a_3 = a_1\cdot (a_2 \cdot a_3)$
- 幺元:$\exists a_0 \in \mathbf{A}, s.t. \forall a \in \mathbf{A}, a_0 \cdot a = a \cdot a_0$
- 逆元:$\forall a \in \mathbf{A},\exists a^{-1} \in A, \quad s.t. \space a \cdot a^{-1}=a_0$
可以验证,三维旋转矩阵对矩阵乘法构成了特殊正交群$SO(3)$——直观意义上接连两次旋转动作认为旋转。
\[SO(3) = \{R \in \mathbb{R}^{3 \times 3} | RR^T = I, det(R) = 1\}\]变换矩阵构成了特殊欧式群$SE(3)$,它也对乘法封闭。
\[SE(3) = \{ T = \begin{bmatrix} R & t \\ {0^T} & 1 \\ \end{bmatrix} \in \mathbb{R}^{4\times 4} | R \in SO(3), t \in \mathbb{R}^{3\times 3}\}\]但是二者对加法都不封闭,即两个变换矩阵相加后并不是旋转矩阵。
李群
李群(Lie group)是具有群结构的光滑微分流形,其群作用与微分结构相容,从抽象上来说,李群就是具有光滑或连续性质的群。对应到我们的问题上,由于三维机器人在空间中移动必然是连续地运动,不可能发生“瞬移”的情形,因而$SO(3)$和$SE(3)$都是李群。
下面由旋转矩阵$R$引出李代数。因为R是随时间连续变化的——相机可看成是连续运动,我们将相机姿态看作是时间$t$的函数,那么自然就有$R(t)R(t)^T = I$成立。上式的左右两侧同时对t求导,我们可得
\[\stackrel{·}{R}(t)R(t)^T + R(t)\stackrel{·}{R}(t)^T = 0\]整理后可得
\[\stackrel{·}{R}(t)R(t)^T = -{( R(t)\stackrel{·}{R}(t)^T )}^T\]如果我们把等式左边看成一个整体,那么我们会发现上式左边是一个反对陈矩阵。
对于任意一个反对称矩阵,我们都由一个向量做反对称变换得到,比如:
\[a^{\wedge} = A = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \\ \end{bmatrix}, \quad A^{\vee} = a = \{a_1, a_2, a_3\}.\]如果将上式左边记为$\phi(t)^{\wedge} = \stackrel{·}{R}(t)R(t)^T \in \mathbb{R}^3$,我们对这个式子两边右乘$R(t)$并注意到$R(t)$的正交矩阵性质,就可以得到:
\[\stackrel{·}{R}(t) = \phi^{\wedge}(t)R(t)\]就好像对$R(t)$求导后其实是左乘了一个$\phi(t)$,而上边这个等式就类似一个一阶微分方程,$\phi$反应了一节导数的性质,它位于正切空间上(tangent space)。我们认为初始值$R(0) = I$,那么就可以解得:
\[R(t) = e^{\phi ^ \wedge t}\]由于这个式子只在$t$附近有效。由此可知,对任意时刻$t$,旋转矩阵$R$和一个向量$\phi$对应,二者满足矩阵指数关系,这个$\phi$就是$SO(3)$上的李代数$so(3)$。因而,为了求$R$,我们只需要求出$exp(\phi t)$即可,这个关系即为指数映射。现在的问题是$so(3)$是如何定义的,指数映射又如何求出呢?
李代数
每个李群都有与之对应的李代数,李代数描述了李群的局部性质。在这个局部正切空间里,一些我们可以找到一些比较好的性质,比如良好定义的加法,从而我们有了良好定义的导数——将李群的导数转化为李代数上的导数,求出来后再转化回去,这就是我们处理李群导数相关内容的基本思路,同时也是研究的重心。
李代数由一个集合$V$, 一个数域$F $和一个二元运算$[\cdot]$ 组成。如果它们满足以下几条性质,则称$(V, F, [\cdot])$ 为一个李代数,记作$g$,其中二元运算$[\cdot]$成为离括号,表达了两个元素的差异。
- 封闭性: $\forall \mathbf{X}, \mathbf{Y} \in V,\ [\mathbf{X}, \mathbf{Y}] \in V$
- 双线性: $\forall \mathbf{X}, \mathbf{Y}, \mathbf{Z} \in V,\ a, b \in F$ , 有 $[a\mathbf{X} +b\mathbf{Y},\ \mathbf{Z}]=a[\mathbf{X}, \mathbf{Z}] + [\mathbf{Y}, \mathbf{Z}],\ [\mathbf{Z},a\mathbf{X} +b\mathbf{Y}]=a[\mathbf{Z},\mathbf{X}] +b[\mathbf{Z},\mathbf{Y}]$
- 自反性: $\forall \mathbf{X} \in V,\ [\mathbf{X}, \mathbf{X}]=\mathbf{0}$
- 雅可比等价:$\forall \mathbf{X},\mathbf{Y},\mathbf{Z} \in V,\ [\mathbf{X},[\mathbf{Y},\mathbf{Z}]] + [\mathbf{Z},[\mathbf{X},\mathbf{Y}]] +[\mathbf{Y},[\mathbf{Z},\mathbf{X}]]=\mathbf{0}$
举例三位向量$\mathbb{R}^3$上定义的叉乘就是一个离括号,其中$g = (\mathbb{R}^3, \mathbb{R}, \times)$就构成了李代数。
李代数$so(3)$
之前提到的$SO(3)$对应的向量$\phi$就是一种李代数,他定义在$\mathbb{R}^3$的向量上。它的反对称矩阵记作:$\mathbf{\Phi} = \phi^\wedge$,那么SO(3)中的向量对应的李括号为:
\[[\phi_1, \phi_2] = (\mathbf{\Phi}_1\mathbf{\Phi}_2 - \mathbf{\Phi}_2\mathbf{\Phi}_1)^{\vee}\]经过验证可以得到上边的式子等价于两向量作外积。
\[[\phi_1, \phi_2] = \phi_1 \times \phi_2\]李代数$se(3)$
与$so(3)$不同的是,$se(3)$定义在$\mathbb{R}^6$空间中。
\[se(3)=\begin{Bmatrix} \mathbf{\xi}=\begin{bmatrix} \mathbf{\rho} \\ \mathbf{\phi} \end{bmatrix} \in R^6,\mathbf{\rho} \in R^3, \mathbf{\phi} \in so(3), \mathbf{\xi}^\wedge=\begin{bmatrix}\phi^\wedge & \mathbf{\rho} \\ \mathbf{0}^T & 0 \end{bmatrix} \in R^{4 \times 4} \end{Bmatrix}\]其中$se(3)$每个元素都称为$\xi$,它是一个六维向量:前三维为平移,记作$\rho$,后三位即为三维旋转向量$\phi$,实质上就是$so(3)$中的元素。另外在$se(3)$ 中, $\wedge$ 符号的含义被拓展了:这里它将一个六维向量转换为四维矩阵,但这里不再表示反对称矩阵,其实这里$\xi$即为变换矩阵的转置。同样,李代数$se(3)$的李括号被定义为:
\[[\xi_1, \xi_2]=(\xi_1^\wedge\xi_2^\wedge-\xi_2^\wedge\xi_1^\wedge)^\vee\]上式经验证后发现,李括号将两个变换矩阵变成了了一个无旋的变换矩阵:
\[[\xi_1, \xi_2] = \begin{Bmatrix} \Phi_1^{\wedge}\rho_2 - \Phi_2^{\wedge}\rho_1 \\ \mathbf{0}_{3\times 3} \end{Bmatrix}\]即旋转部分被抹去,只剩下平移部分,而平移部分是由原来两个元素中的旋转和平移部分组合得到的。
指数映射和对数映射
李群到李代数之间是一个指数映射(反之是对数映射),通过借助这个指数映射我们可以将大量在李群上不好解决的问题转嫁到李代数上解决,之后再映射回去间接得到李群上的答案。
$SO(3)$上的指数映射
我们利用关系李群和李代数之间的关系:
\[\stackrel{·}{R}(t) = \phi^{\wedge}(t)R(t)\]可知求出起初指数映射,就能得到李群上的导数。求指数映射我们需要用到泰勒展开式。任意矩阵的指数映射都可以写成一个泰勒展开式,这个展开式只有在收敛的情况下才有解,结果仍然是一个矩阵。所以对于$so(3)$中的元素$\phi$,其指数映射可以写成
\[exp(\phi^{\wedge}) = \sum\limits_{n=0}^\infty\frac{1}{n!}(\phi^\wedge)^n\]我们定义$\phi = \theta \mathbf{a}$,其中$\theta$和$a$分别是$\phi$的模长和单位向量。我们可以验证:
\[\mathbf{a}^\wedge \mathbf{a}^\wedge=\mathbf{a}\mathbf{a}^T-\mathbf{I} \\ \mathbf{a}^\wedge \mathbf{a}^\wedge \mathbf{a}^\wedge=-\mathbf{a}^\wedge\]以上两个式子提供了我们对泰勒展开式中高次项化简的方法。 那么我们对上边泰勒展开式化简可以得到:
\[\exp{\phi^\wedge}=\exp(\theta \mathbf{a})=\sum\limits_{n=0}^\infty \frac{1}{n!}(\theta \mathbf{a}^\wedge)^n \\ =\cos\theta\mathbf{I} + (1-\cos\theta)\mathbf{a}\mathbf{a}^T + \sin\theta\mathbf{a}^T\]这和之前的罗德里格斯公式有着相同的形式,标明$so(3)$实际上就是由旋转向量组成的空间,而指数映射其实就是罗德里格斯公式。那么与之对应的对数映射,给定旋转矩阵,我们就可以求李代数,将$SO(3)$映射到$so(3)$上:
\[\phi=\ln(R)^\vee=(\sum\limits_{n=0}^\infty\frac{(-1)^n}{n+1}(\mathbf{R}-\mathbf{I})^{n+1})^\vee\]但是实际上没必要这样求,因为旋转向量已经介绍了矩阵到向量的转换关系:
\[\theta = \arccos{\frac{tr(\mathbf{R}) - 1}{2}} \\ \mathbf{R}n = n\]这里需要注意的是,指数映射是一个满射,即每个$SO(3)$中的元素都可以找到一个$so(3)$里的元素与之对应;但是泛指不成立,因为多旋转一圈的旋转向量对应的李代数是相同的。但是如果把旋转角固定在$[0, 2\pi]$之间,那么李群和李代数的元素就是一一对应的。
$SE(3)$上的指数映射
下面是推导结果:
\[\exp(\xi^\wedge)=\begin{bmatrix} \sum\limits_{n=0}^\infty\frac{1}{n!}(\phi^\wedge)^n & \sum\limits_{n=0}^\infty\frac{1}{(n+1)!}(\phi^\wedge)^n\rho \\ \mathbf{0}^T & 1 \\ \end{bmatrix}= \begin{bmatrix} \mathbf{R} & \mathbf{J}\rho \\ \mathbf{0}^T & 1 \\ \end{bmatrix}=\mathbf{T}\]其中$exp(\xi^{\wedge})$的左上角是SO(3)的元素,即旋转部分。矩阵$\mathbf{J}$则为:
\[\mathbf{J} = \frac{\sin\theta}{\theta}\mathbf{I}+(1-\frac{\sin\theta}{\theta})\mathbf{a}\mathbf{a}^T+\frac{1-\cos\theta}{\theta}\mathbf{a}^\wedge\]这个公式与落地里格斯公式类似,$\xi$中的平一部分经过$\rho$指数变换后,发生了一次以$\mathbf{J}$为系数的线性变换。
相反的,$SE(3)$到$se(3)$也有相应的对数映射,但是我们一般不用,我们一般利用左上角的旋转矩阵计算出旋转向量,再用右上角的平移向量得到$\rho$。
李代数求导与扰动模型
李代数与李群的计算对应关系
我们由于李群没有加法讨论出来了李代数,我们想要利用李代数的加法定义李群的导数,再利用指数映射和对数映射完成变换关系。但是还有一个基本问题,就是在李代数上做加法,是否就等价于在李群上做乘法呢?
\[exp(\phi_1^{\wedge})exp(\phi_2^{\wedge}) = exp({(\phi_1 + \phi_2)}^{\wedge})\]上式在标量的情况下显然是成立的,但是现在指数上式矩阵,结果很遗憾是不成立的。我们由BCH(Baker-Campbell-Hausdorff)公式给出:
\[\ln(\exp(\mathbf{A})\exp(\mathbf{B}))=\mathbf{A}+\mathbf{B}+\frac{1}{12}[\mathbf{A},\mathbf{B}]+\frac{1}{12}[\mathbf{A},[\mathbf{A},\mathbf{B}]]-\frac{1}{12}[\mathbf{B},[\mathbf{A},\mathbf{B}]]+\ldots\]其中$[\cdot]$为李括号,可以看到,两个矩阵指数的乘积结果的指数项,是两个矩阵之和再加上一些由李括号组成的余项。
我们在求导数的时候,其中一项肯定是小量,可以看成相机连续两帧之间的位姿变化,利用这个小量,我们就可以对上边的式子进行优化:
\[\ln(\exp(\phi^\wedge_1)\exp(\phi^\wedge_2))^\vee \approx \begin{cases} \mathbf{J}_l(\phi_2)^{-1}\phi_1 + \phi2,\ 当\phi_1 为小量\\ \mathbf{J}_r(\phi_1)^{-1}\phi_2 + \phi_1,\ 当\phi_2 为小量\\ \end{cases}\]上边的优化结果分别对应着$\phi_1$和$\phi_2$为小量时的近似状态,我们分别称为左乘模型和右乘模型。之所以要区分做成还是右乘模型,是因为其中的$\mathbf{J}_l$和$\mathbf{J}_r$是不一样的。对于左乘BCH近似模型,雅可比矩阵$\mathbf{J}_l$就是:
\[\mathbf{J}_l = \mathbf{J} = \frac{\sin\theta}{\theta}\mathbf{I}+(1-\frac{\sin\theta}{\theta})\mathbf{a}\mathbf{a}^T+\frac{1-\cos\theta}{\theta}\mathbf{a}^\wedge\]它的逆为:
\[\mathbf{J}_l^{-1}=\frac{\theta}{2}\cot\frac{\theta}{2}\mathbf{I}+(1-\frac{\theta}{2}\cot\frac{\theta}{2})\mathbf{a}\mathbf{a}^T-\frac{\theta}{2}\mathbf{a}^\wedge\]而对于右乘模型,右乘雅可比矩阵就是将左乘雅可比矩阵的自变量取负号。
\[\mathbf{J}_r(\phi) = \mathbf{J}_l(\phi)\]现在来小结一下,假如有一个旋转矩阵$\mathbf{R}$,对应的李代数为$\phi$,现在对它有一个微小的扰动,记作$\mathbf{\Delta R}$,对应的李代数为$\Delta \phi$。那么在李群上,新的旋转矩阵即为$\mathbf{\delta R \cdot R}$,而在李代数上,新的李代数为$\mathbf{J}_l^{-1}\Delta \phi + \phi$,即:
\[\exp(\phi^\wedge)\exp(\Delta\phi^\wedge)=\exp((\phi+\mathbf{J}_l(\phi)^{-1}\Delta\phi)^\wedge)\]反之,如果我们在李代数上做加法,那么可以近似为李群上带左/右雅可比矩阵的乘法:
\[exp((\phi + \Delta \phi)^\wedge) = exp((\mathbf{J_l}\Delta\phi)^\wedge)exp(\phi^\wedge) = exp(\phi^\wedge)exp((\mathbf{J_r}\Delta\phi)^\wedge)\]至此,我们可以讨论一下怎么求没有良好定义加法的李群上的导数:
- 利用李代数表示位子,然后根据李代数的加法对李代数进行求导。(导数模型)
- 对李群来左乘或右乘微小扰动,并对这个扰动的李代数求导。(扰动模型)
求导模型
假设空间点$\mathbf{p}$进行了一次旋转$\mathbf{R}$,得到了新的点$\mathbf{Rp}$,要计算旋转后的点相对于旋转的导数,可以不严谨得写为:
\[\frac{\partial(\mathbf{R}\mathbf{p})}{\partial\mathbf{R}}\]设$\mathbf{R}$对应的李代数为$\phi$,就可以写成:
\[\frac{\partial(\mathbf{R}\mathbf{p})}{\partial\mathbf{R}} = \frac{\partial(\exp(\phi^\wedge)\mathbf{p})}{\partial\phi}\]按照导数的定义并利用一阶泰勒展开以及BCH公式,就可以得到:
\[\frac{\partial(\exp(\phi^\wedge)\mathbf{p})}{\partial\phi}=\lim_{\delta\phi\to0}\frac{\exp((\phi+\delta\phi)^\wedge)\mathbf{p}-\exp(\phi^\wedge)\mathbf{p}}{\delta\phi}=-(\mathbf{R}\mathbf{p})^\wedge\mathbf{J}_l\]这个公式时直接对旋转矩阵$\mathbf{R}$进行求导,最后结果含有左雅可比矩阵$\mathbf{J_l}$。当然,我们自然希望避免计算雅可比矩阵,所以我们一般选用下边的扰动模型。
扰动模型
假设某空间点$\mathbf{p}$ 经过了一次变换$\mathbf{T}$,对应的李代数为$\xi$,得到$\mathbf{Tp}$。给 $\mathbf{T}$左乘一个微小扰动$\mathbf{\Delta T}$,扰动项的李代数为$\delta \xi = [\delta \rho , \delta \phi]^T$。则有:
\[\frac{\partial(\mathbf{T}\mathbf{p})}{\partial\delta\xi}=\lim_{\delta\xi\to0}\frac{\exp(\delta\xi^\wedge)\exp(\xi^\wedge)\mathbf{p}-\exp(\xi^\wedge)\mathbf{p}}{\delta\xi}= \begin{bmatrix} \mathbf{I}_{3\times3} & -(\mathbf{R}\mathbf{p} + \mathbf{t})^\wedge_{3\times3} \\ \mathbf{0}^T_{1\times3} & \mathbf{0}^T_{1\times3}\\ \end{bmatrix}=(\mathbf{T}\mathbf{p})^\bigodot\]最后结果被定义为了运算符号$\bigodot$,把一个齐次坐标下的空间点变换成一个4*6 的矩阵。